Let’s understand this with a story.
Alice,Bob, and john are best friends, Let’s assume Alice and Bob took a programming course this semester and john didn’t. john went to hangout with alice and bob. conversation goes like this.
John: “Hey Alice what are you doing ?”
Alice: “We are writing programs for our assignments."
John: “Hey Bob are You coding the same problem ?"
Bob:“Yes."
John: “It’s look like alice code is more efficient than your’s isn’t it?"
Bob:“Why do you think so ?"
John:“As length of her program is lesser."
Bob: “we can’t compare two Algorithm by just number of lines of code ."
John: “why?"
Bob: “Suppose if i have written a program in c in 100 lines then i can write same program in python in 20 lines or less that doesn’t mean
c program is less efficient than python”
John: “Then you must be comparing it with running time. right ? “
Bob: " Nope .we can not compare two Algorithm by execution time."
John: “why ?"
Bob: “Because suppose Alice computer is faster than mine .
My computer will take more time to run than her."
John: “What if we run both program on same computer ?"
Bob: “Well, there are a lot’s of processes running at same time.
suppose i am playing a game and running this program same time
then game is hogging all my memories that might slow my program.
even if i would run same program on my computer multiple times,
execution time would be different each time and the differnce
between these execution time would be random. to compare them by execution time you must have to determine CPU time."
John:“Then Why don’t you calculate CPU time ?"
Bob:“Measuring CPU time is difficult. If you are running on a multi-user machine, then elapsed time is not the correct measure. You must measure CPU time. But for certain programming languages, additional features might run at unpredictable results and you may not wish to include these in your measurements. For example, if you use Java, the Java garbage collector will run at various points to reclaim the memory space used
by unneeded objects. You may want to exclude from your measurements any
time spent garbage collecting. Another problem is that the timing commands
provided by many programming languages do not report times to a sufficient
level of precision. for most problems there can be many bottleneck
test cases you have to find out CPU time of program for each test case and then take average of that to find out execution time."
John: “Then what is best way to compare two Algorithms ?"
Bob: “There is a notation called asymptotic notation to measure efficiency of Algorithm."
John: “It sounds like complex. can you explain it in simple way ?"
Bob: " it’s not complex . in asymptotic notation
we always talk about rate of growth of program.rate of growth means
how does the execution time changes as the size of input grows.
for example if you have to print a number from 1 to n then it will
take linear time why ? because run time of your program is proportional to n .
how do you know that ? suppose if n is 10 then your print statement will
execute 10 times if i change n to 100 then print statement will execute 100 times.
as n is grows 10 times your task of printing is also grows 10 times."
now you'll have basic understanding how to compare two programs. now you would be thinking why we care about efficiency it is not sufficient my program is giving correct output ?. suppose if you want to buy some product on Amazon and amazon takes 10s or more each time whenever you click on some option. would you use it in 2018 ? yes you won't. now if you're thinking how to predict how much time a program will take to execute in general then skim through the following functions and their rate of growth with respect to input size 'n'
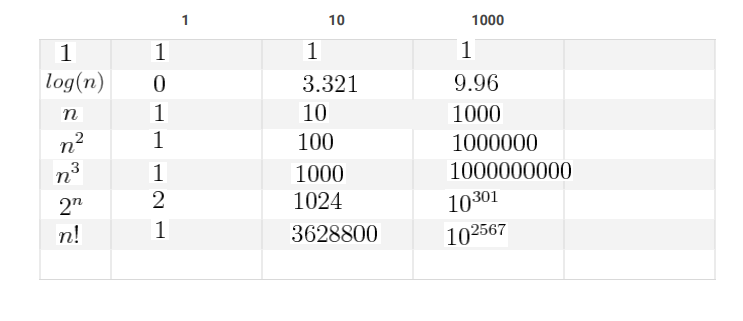
a normal computer can execute 109 instruction per second. suppose we have two algorithm and you are going to run both for input size 1000 and one algorithm has time complexity of O(n) then how much second computer will take to give you result ? 1000/109 = 1 micro second but it is not exact value it would took few mili seconds in worst case. and other hand we take second algorithm for same input size with different time complexity lets take O(2n) then it will take 21000/109 = 10301/109 > 10290 seconds if we divide it by number of seconds in a year(3 * 107) which will still > 10280 years which is more than 10269 times of age of universe , you don't want to write such algorithms for real world problem.then what is solution ? chose algorithm that fulfill your needs. to know which algorithm will fulfill your needs you should know how to measure complexity of algorithm. There are two types of complexity that we talk about for algorithms 1.Time Complexity 2.Space Complexity
1.Time Complexity: let’s talk about how to find Time complexity of a program . consider following code snippet.
#include<stdio.h>
int main(){
int n;
scanf("%d",&n);
while(n>0){
printf("%d\n",n);
n--;
}
return 0;
}
yes we can still find out three cases
1.maximum how many times loop will be executed.(worst case)
2.minimum how many times loop will be executed.(best case)
3.average how many times loop will be executed.(average case)
what will be the minimum number of times while loop will be executed ? 0 times .when n<=0.what will be the maximum number of times while loop will be executed ? n times (n would be max size of int) now what will be the average number of times while loop will be executed ? (0+n)/2 = n/2 times.In asymptotic notations we do similar analysis.There are three most often used asymptotic notations are following
1.Big O ( for worst case)
2.Omega ( for best case)
3.Theta ( for average case)
suppose You have bought a Macbook pro in 1499$ . and one of your friend asked you how much did it cost ? what would you say ? 1500$ right ? (unless you have a friend which would tell you i could have bought this for you for free . moreover he would have made you CEO of apple .)
why did you say that ? because 1499$ was huge compare to 1$ you can neglect it. similarly most of the time we are neglecting some constants or less dominating terms in this analysis. for e.g You have a function f(x) = n3 + n + 1 is can be equal to n3 by multiplying some constants into it. it will be more clear when we move further. let's discuss about Asymptotic notations.
1.Big O notation (upper bounding function): we represent worst case complexity of an algorithm using this notation. suppose you have a function f(x) then what would be the upper bounding function of f(x)? upper bounding function mean the function which gives f(x) maximum rate of growth for large input .
for example f(x) = n3 + n + 1 for larger value of n , n3 would give more rate of growth to f(x) than n and 1 hence n3 is upper bounding function of f(x) let's denote upper bounding function with g(x) then mathematically
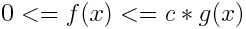
where c can have infinte numbers of values , c>0
e.g: f(x) = 2n + 4
what would be g(x) ?
in 2n and 4 , 2n have higher rate of growth hence g(x) = n
what will be c? 2n+4<=cn
for c<=2 cn could never greater or equal to f(x), let’s take c=3
2n+4<=3n when n>=4 hence 2n+4 = O(n)
after some value of n ,c*g(x) will be always >= f(x)
so any function which is asymptotically greater than g(x) will be also upper bounding function of f(x).e.g 2n+4 = O(n2) but most of the time we are interested in tightest upper bounding function which is O(n)
2.Omega notation (lower bounding function): we represent best case complexity of an algorithm using this notation. suppose you have a function f(x) then the lower bounding function mean the function which gives the largest rate of growth which is less than or equal to the rate of growth of f(x) for example f(x) = n3 + n + 1 for larger value of n , n3 would give less than the of growth to f(x) hence n3 is upper bounding function of f(x) let’s denote lower bounding function with g(x) then mathematically
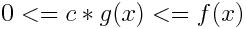
where c can have infinte numbers of values
e.g: f(x) = 2n + 4
what would be g(x) ?
n have rate of growth less than f(x) hence g(x) = n
what will be c? 2n+4>=cn
c<=2 cn could never greater than f(x),take c=2
2n+4<=2n when n>=0 hence 2n+4 = Ω(n)
3.theta notation (order function): We represent average complexity of an algorithm using this notation. This notation decides whether upper and lower bounds of a function is same. if upper and lower bounds of a function is same then theta would be also same. mathematically
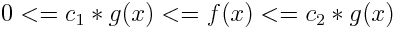
where c1<=2 and c2>=3 and c1,c2>0
e.g: f(x) = 2n + 4
f(x) = O(n)
f(x) = Ω(n)
f(x) = Θ(n)
#include<stdio.h>
int main(){
{
// block 1 n
}
{
// block 2 n^2
}
{
// block 3 1
}
return 0;
}
for(i=0;i<n;i++) // 1st block
{
printf("hello world !");
}
for(i=0;i<n;i++) // 2nd block
{
for(j=0;j<n;j++)
{
printf("hello world !");
}
}
in 2nd block how many times outer for loop gets executed ? n times and for each outer loop iteration inner loop also get executed n times hence total cost would be n*n = n2, time complexity O(n2) for worst case.what will be the best case time complexity ? when n<=0 loop will execute 0 times hence best case time complexity will be Ω(1) , in average case for loop will be executing (0+n2)/2 = n2/2 times so average time complexity would be Θ(n2)
for(i=0;i<n;i++) // 3rd block
{
printf("hello world !");
if(i==2){
break;
}
}
for 3rd block how many times for loop get executed ? maximum 3 times i=0 to i=2 right ? due to break statement loop will be broken when i reaches 2, time complexity O(1) .
for(i=1;i<n;i=i*2) // 4th block
{
printf("hello world !");
}
for 4th block how many times for loop get executed ?
take few examples to convience yourself . value of i will be increasing from 1 till i<n.
1 2 4 8 2k when will be 2k > n . take log base 2 both sides
log2(2k)>log2(n)
k >log2(n)
so this loop will be executing around log2(n) times. time complexities would be O(log(n)), Ω(1) and
Θ(log(n))
what if i start at i=0 ? how many times this loop would be executed ? forever right ? if n>0
for(i=1;i<10;i++) // 5th block
{
printf("hello world !");
}
for 5th block how many times for loop get executed ? 10 times because here no matter what is input size it will always run 10 times. so this is constant time operation time complexity O(1).but if our input size is <= 10k and value of constant is >= 10k then constant would affect execution time.
j=0;
for(i=0;i<n;i++) // 6th block
{
for(;j<n;j++)
{
printf("hello world !");
}
}
for 6th block how many times for loop get executed ? for i=0 inner loop will execute n times after that inner loop will not executed why ? because unlike 2nd block we are not initializing j for each i . so how may times loop will be executed ? 1*n ( first time i=0 inner loop will execute n times and outer loop will executed 1 times) + n-1( i=1 to n-1) times = 2n-1 now we will eliminate constants so it will become n , time complexities O(n),Ω(1) and Θ(n)
void merge(int a, int b, int low,int mid, int high)
{
// some O(n) operation
}
void mergesort(int a, int b, int low, int high) // T(n)
{
int mid;
if(low<high)
{
mid=(low+high)/2; // O(1)
mergesort(a,b,low,mid); // T(n/2)
mergesort(a,b,mid+1,high); // T(n/2)
merge(a,b,low,mid,high); // O(n)
}
}
For recursive function:
for recursive function like above you need to calculate time complexity using back substitution algorithm. lets see how this works.
suppose time complexity of this function is T(n)
then how can we write T(n)?
T(n) = 2T(n/2) + cn —- (1) (neglected O(1) operation)
T(n/2) = 2T((n/2)/2) + cn/2
T(n/2) = 2T(n/4) + cn/2
now substitute value of T(n/2) into equation (1) we will get
T(n) = 2 * 2T(n/4) + 2* cn/2 + cn
T(n) = 4T(n/4) + 2cn
from above observation you would get following result
T(n) = 2k*T(n/2k) + kcn
when n=1 then T(n)=1
so, n/2k = 1
2k = n
k = log2(n)
on substituting value k in T(n) ,T(n) = 1 + log(n)*c*n
so time complexity would be O(nlogn)
we can also calculate this using master’s theorem also but this is
more generalized method.
2.Space Complexity:
if you have learned above concepts then you already know how to calculate sapce complexity . This article become long that’s why i wouldn’t discussed this. for 5 min read go to this link